Bézier curves
A Bézier curve is defined by a set of control points \(P_0\) through \(P_n\).
Linear Bézier curve

Given distinct points \(P_0\) and \(P_1\), a linear Bézier curve is simply a line between those two points and is equivalent to linear interpolation.
\[B_{P_0,P_1}(t) = P_0 + t ( P_1 − P_0 )\]def liear_bezier(p0, p1, t):
return lerp(p0, p1, t)Quadratic Bézier curve
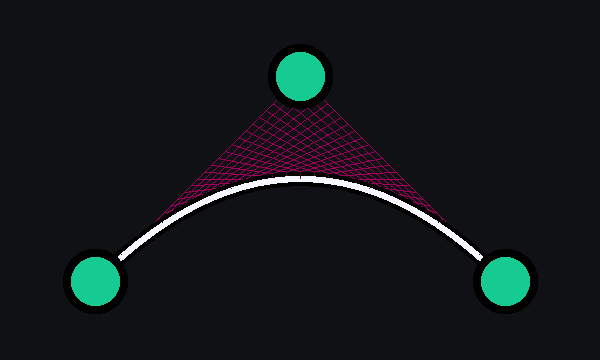
A quadratic Bézier curve is the path traced by the function \(B(t)\), given points \(P_0\), \(P_1\), and \(P_2\), which can be interpreted as the linear interpolant of corresponding points on the linear Bézier curves from \(P_0\) to \(P_1\) and from \(P_1\) to \(P_2\) respectively.
\[B_{P_0,P_1,P_2}(t) = (1−t) B_{P_0,P_1}(t) + t B_{P_1,P_2}(t)\]def quadratic_bezier(p0, p1, p2, t):
v0 = liear_bezier(p0, p1, t)
v1 = liear_bezier(p1, p2, t)
return lerp(v0, v1, t)Cubic Bézier curve
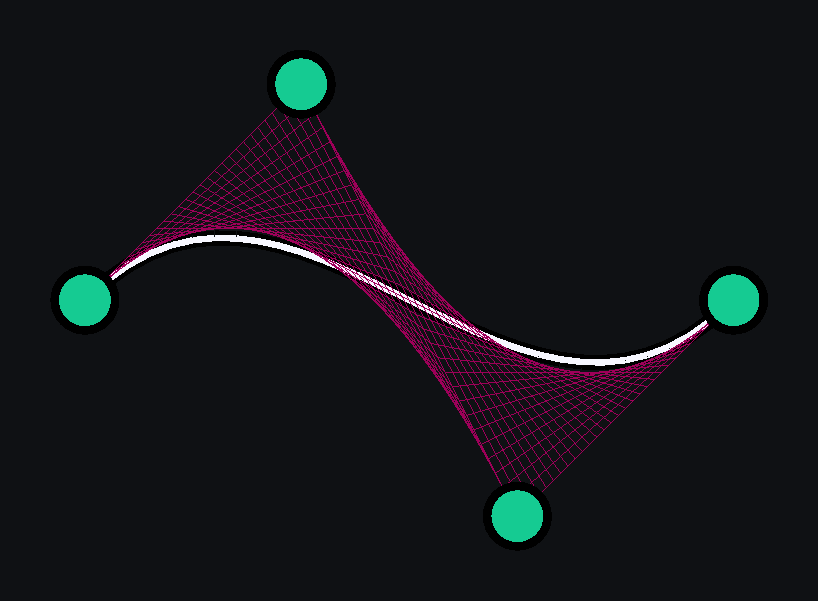
Four points \(P_0\), \(P_1\), \(P_2\) and \(P_3\) define a cubic Bézier curve. The curve starts at \(P_0\) going toward \(P_1\) and arrives at \(P_3\) coming from the direction of \(P_2\). The cubic Bézier curve can be defined as an affine combination of two quadratic Bézier curves.
\[B_{P_0,P_1,P_2,P_3}(t) = (1−t) B_{P_0,P_1,P_2}(t) + t B_{P_1,P_2,P_3}(t)\]def cubic_bezier(p0, p1, p2, p3, t):
v0 = quadratic_bezier(p0, p1, p2, t)
v1 = quadratic_bezier(p1, p2, p3, t)
return lerp(v0,v1,t)Check out the code on GitHub.
Read more about Bézier curves on Wikipedia.